Equivalent Springs

This is an excerpt from Layton Hale’s lecture notes “Design and Analysis of Constraint Systems” from the November 2010 ASPE Conference.

Many engineers make a simple mistake when determining the equivalent stiffness of a spring that is rotated with respect to a coordinate system. Typically they find $k_x=k \cos{\theta}$ and $k_y=k \sin{\theta}$ , which are both incorrect.

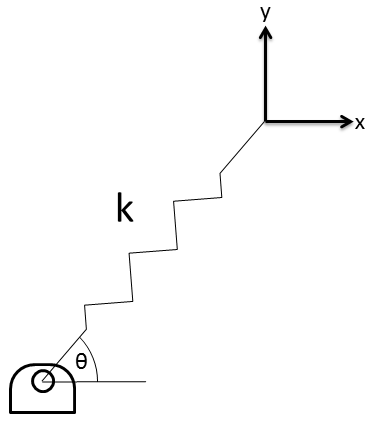
When we displace the spring in the x direction $\delta_x$ the compression of the spring along it’s axis is quite a bit less as you can see in the figure below. From the figures it is quite easy to see:

$\delta_x = \delta / \cos{\theta}$

$\delta_y = \delta / \sin{\theta}$

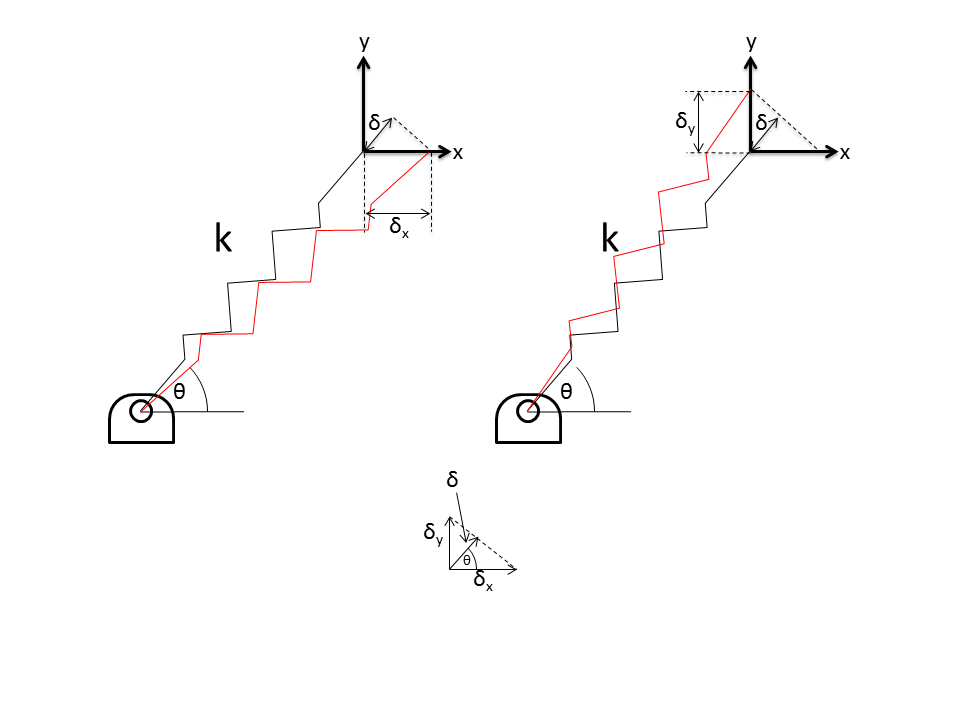It follows that the spring stiffness along the x-direction is:

$\begin{matrix}k_{xx}&= &\frac{F_x}{\delta{x}}\\k_{xx}& = &\frac{F\cos{\theta}}{\delta/\cos{\theta}}\\k_{xx}& = &\frac{F}{\delta}\cos^2{\theta}\end{matrix}$

We can then easily solve for the equivalent stiffness matrix as:

$\mathbf{K} = k\cdot \begin{bmatrix} \cos^2{\theta} & \cos{\theta}\cdot\sin{\theta}\\ \cos{\theta}\cdot\sin{\theta} & \sin^2{\theta} \end{bmatrix}$

And now we can compute the forces along the rotated coordinate system as:

$\begin{bmatrix}f_x\\ f_y\end{bmatrix} = \begin{bmatrix}k_{xx} & k_{xy}\\ k_{yx} & k_{yy}\\\end{bmatrix}\cdot\begin{bmatrix}\delta_x\\ \delta_y\end{bmatrix}$

Post Navigation