A client needed to determine the performance of a leadscrew actuator. A sensitive optical sensor quickly moves to various positions and holds very still once in position, even in the presence of external disturbances.
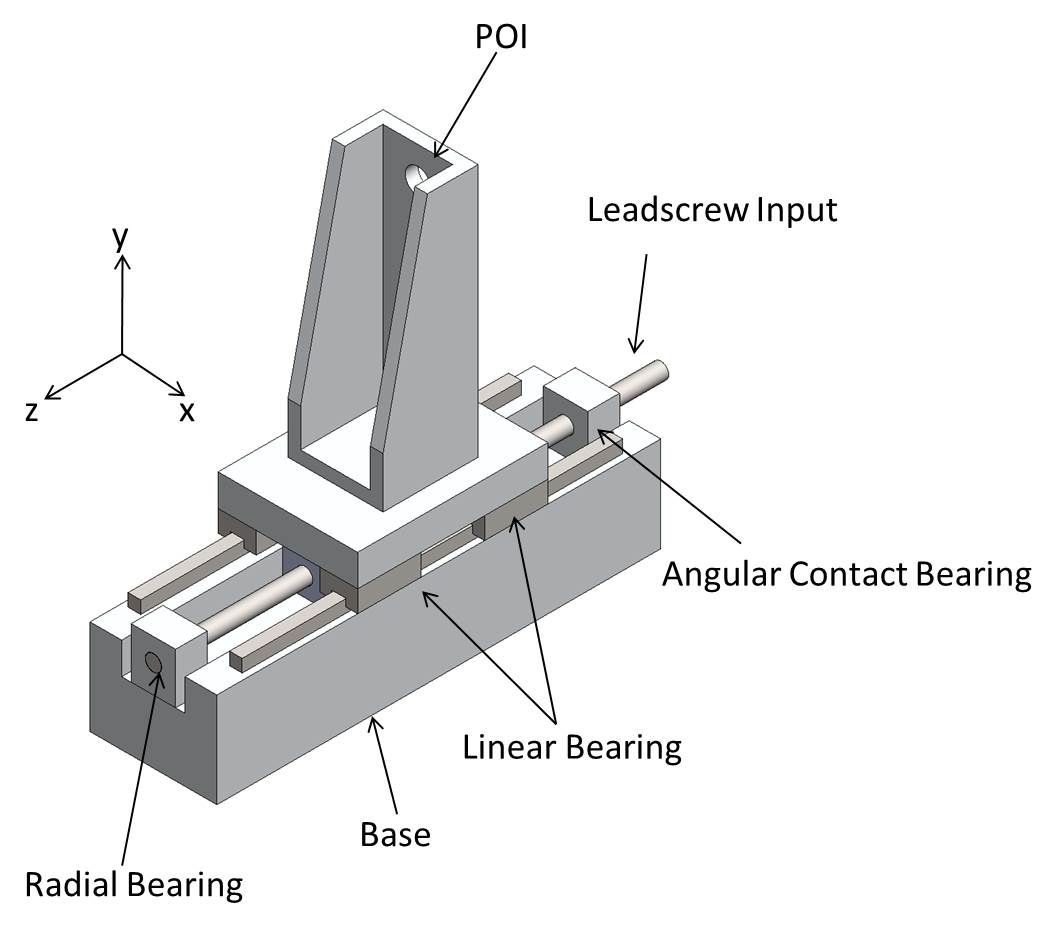
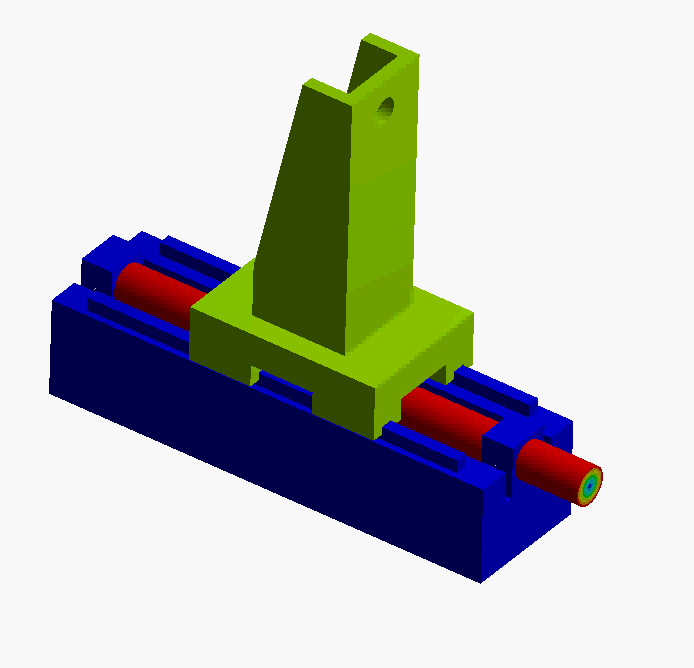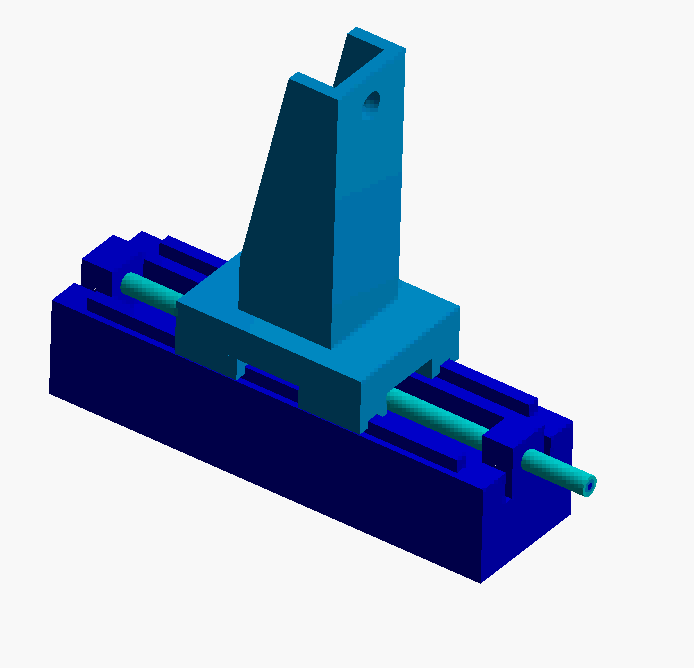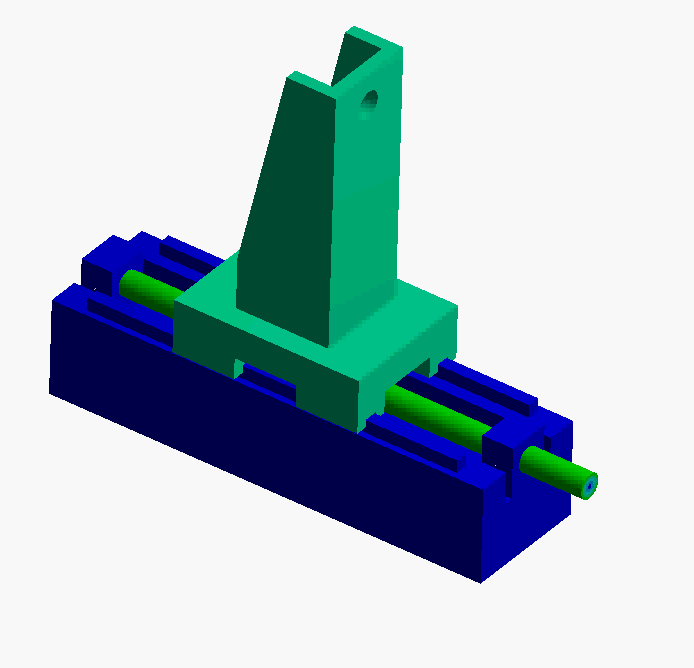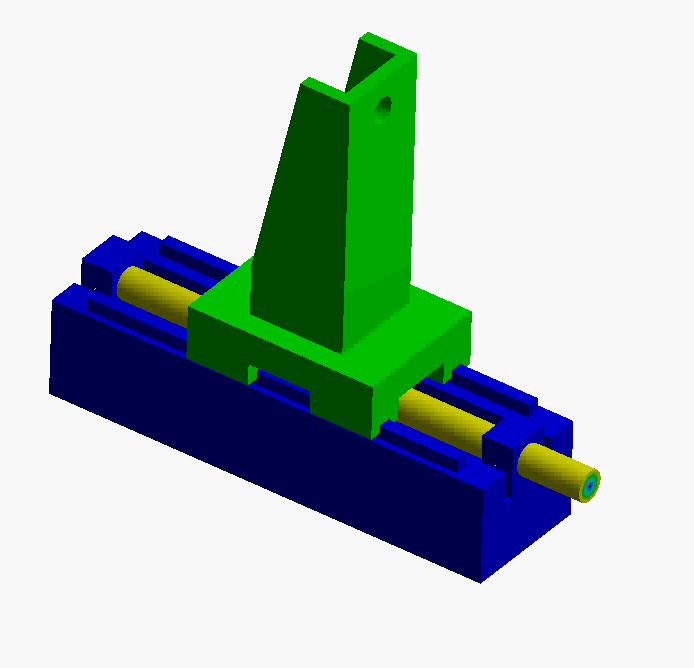
A simplified representation of the leadscrew actuator is shown below. A DC motor applies torque at the leadscrew, moving the carriage along the z-axis. In this particular case we are concerned with accurate positioning of the POI where a sensitive optical sensor is mounted. Note: in our simplified model, it is modeled as a hole.
The position requirements are:
- travel = 200 mm
- velocity = 2 m/s
- acceleration = 5 g ≈ 50 m/s2
- jerk = 10,000 m/s3
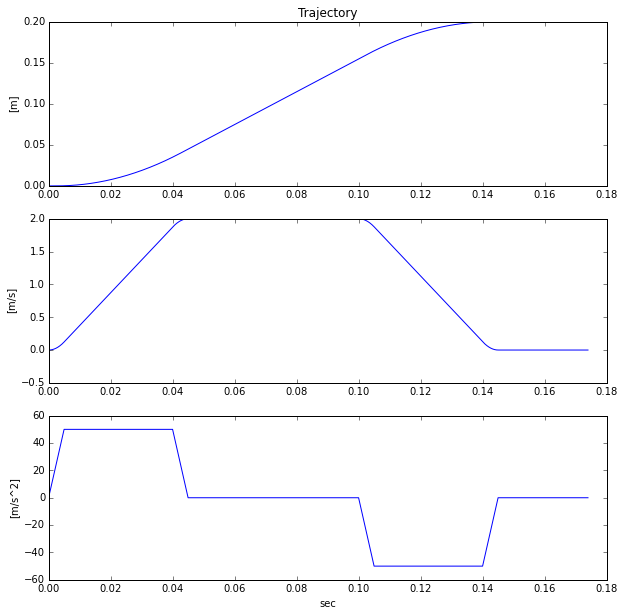
And the base disturbances are summarized as:
| Base Input Direction | 0-10 Hz | 10-500 Hz | 500-5000 Hz |
|---|---|---|---|
| X-Dir [(nm/s2)2/hz] | 0.11 | 25.0 | 0.01 |
| Y-Dir [(nm/s2)2/hz] | 0.15 | 50.0 | 0.01 |
| Z-Dir [(nm/s2)2/hz] | 0.14 | 30.0 | 0.01 |
| RX-Dir [(nrad/s2)2/hz] | 0.10 | 150.0 | 0.005 |
| RY-Dir [(nrad/s2)2/hz] | 0.10 | 70.0 | 0.005 |
| RZ-Dir [(nrad/s2)2/hz] | 0.10 | 15.0 | 0.005 |
The optical sensor must not exceed the stability requirements listed in the table below:
| X-Dir [μm] | Y-Dir [μm] | Z-Dir [μm] | Rx-Dir [μrad] | Ry-Dir [μrad] | Rz-Dir [μrad] | |
|---|---|---|---|---|---|---|
| Stability Reqs. | 1.0 | 1.0 | 1.0 | 5.0 | 5.0 | 5.0 |
First, the system mode shapes are calculated using FEA modal analysis:
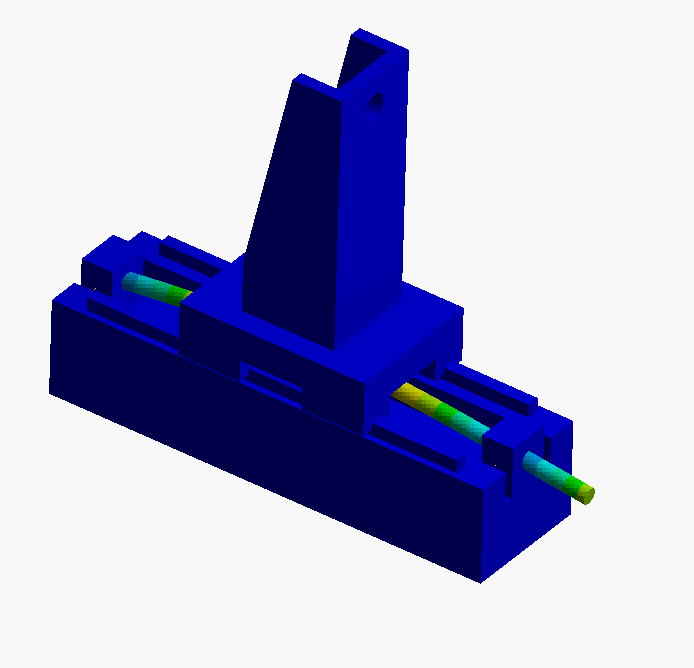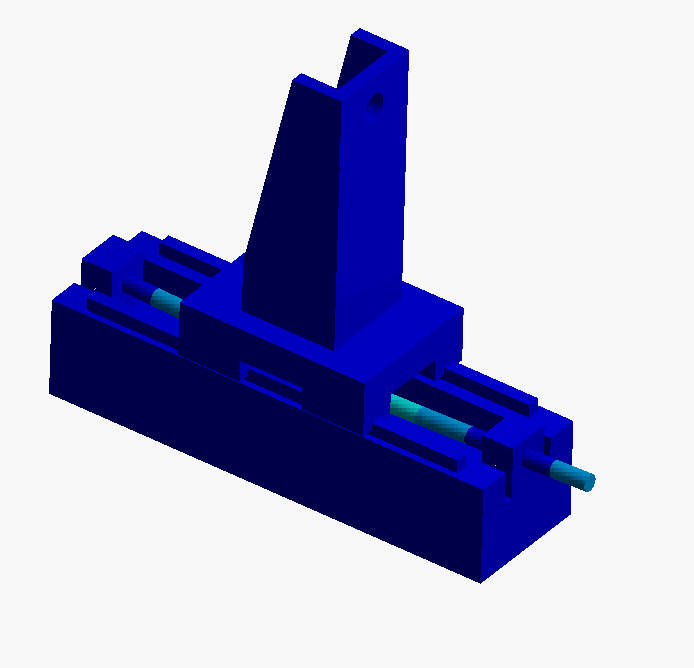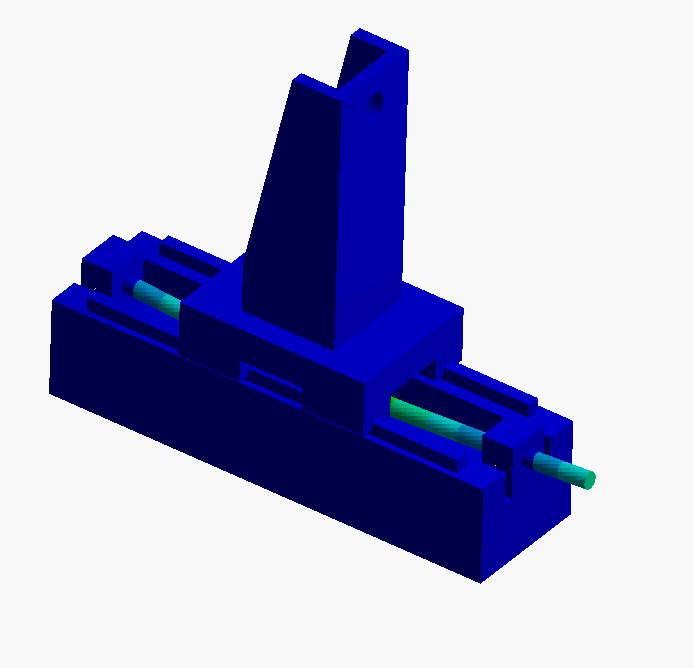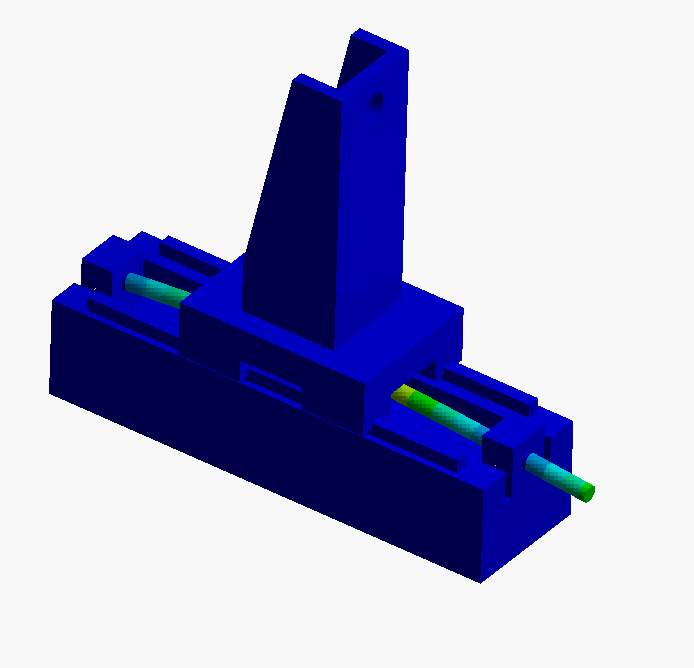
- Mode 1: This is a rigid body mode, screw rotation translates into carriage motion along the bearing. The lead of the screw dictates the motion.
- Mode 2 & 3: In these two modes the leadscrew is bending in the horizontal and vertical planes. This is the first mode that would impact servo positioning performance. To improve the dynamics, we would need to design a stiffer leadscrew (larger diameter, shorter screw, etc.)
- Mode 4, 5, 6: In these modes the carriage is rocking on the linear ball-guide bearings. To improve these dynamics some of the possibilities are:
- move carriage center-of-mass to the center of the bearings
- widen the bearing spacing
- lighten the carriage mass
- select stiffer bearings
- design a tuned mass damper to dampen these modes
 |
 |
 |
 |
 |
 |
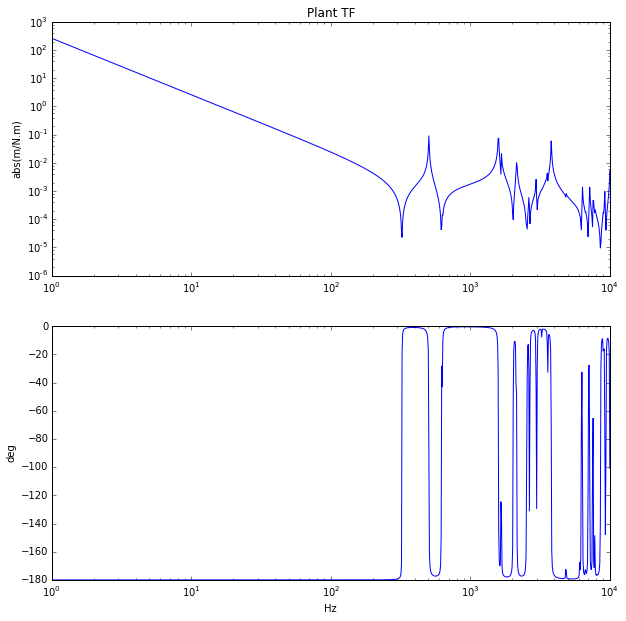
Once the mode shapes are calculated, we have the system Eigenvalues and Eigenvectors and can calculate the system state space model (ABCD matrices). The frequency response from torque input on the leadscrew to the screw rotation is shown below. Since the input and output are co-located the phase is always between 0 deg and -180 deg, quite easy to make a stable system.
Adding a simple lead controller with low pass filter get’s a crossover frequency of 75Hz and phase margin of 45 deg.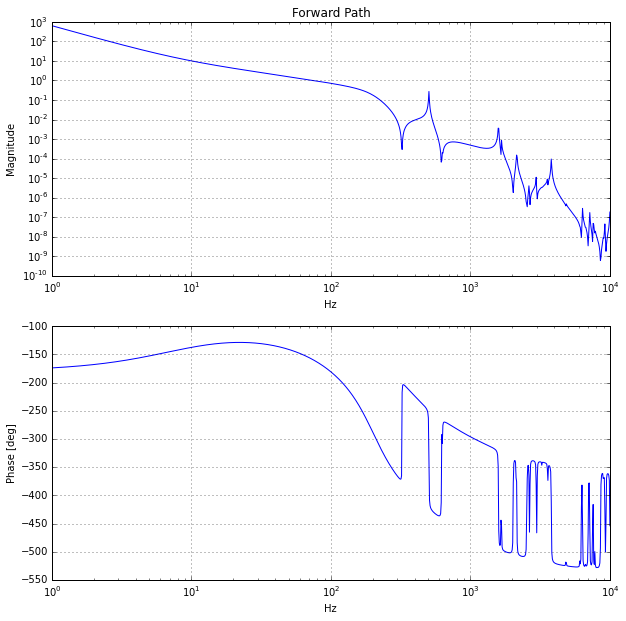
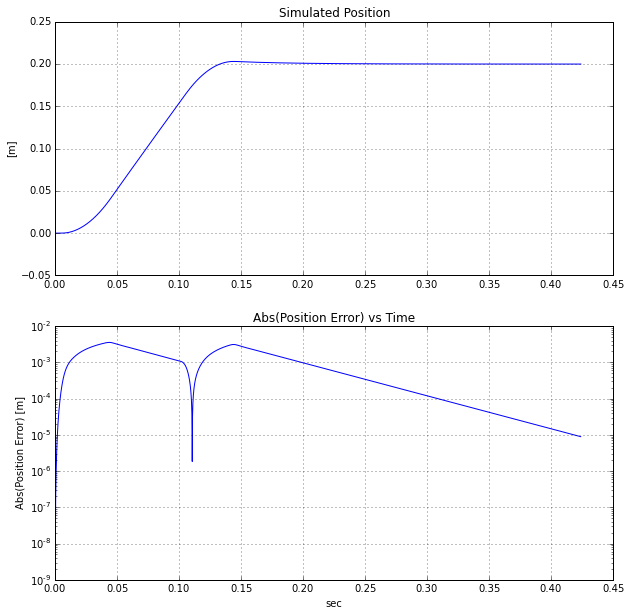
Now that we have the closed-loop model we can simulate the transient response as shown below:
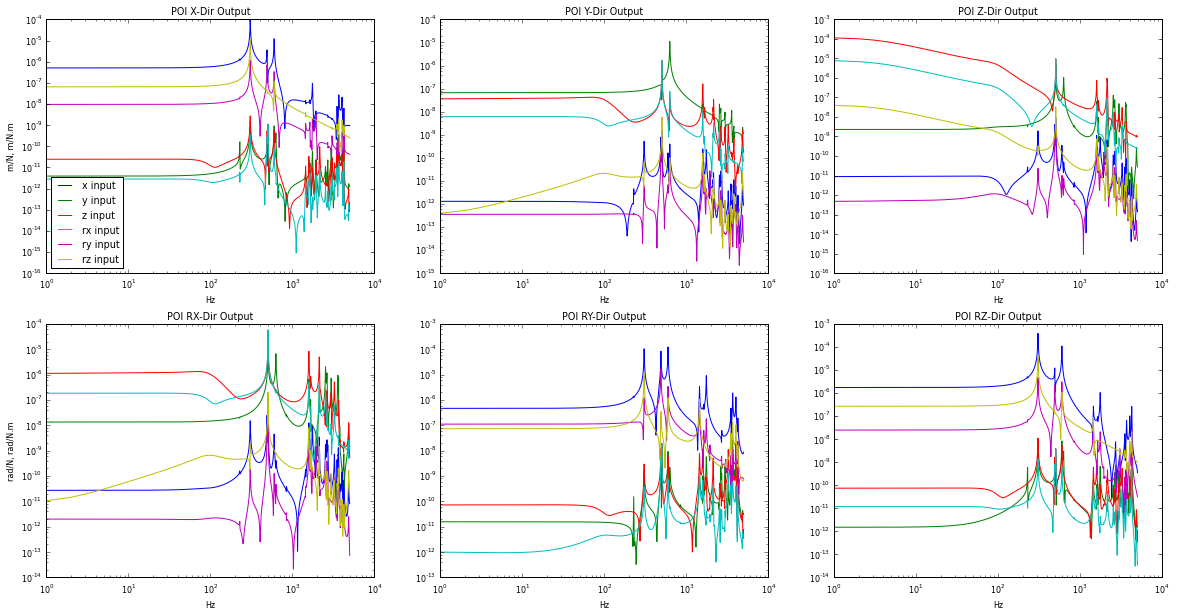
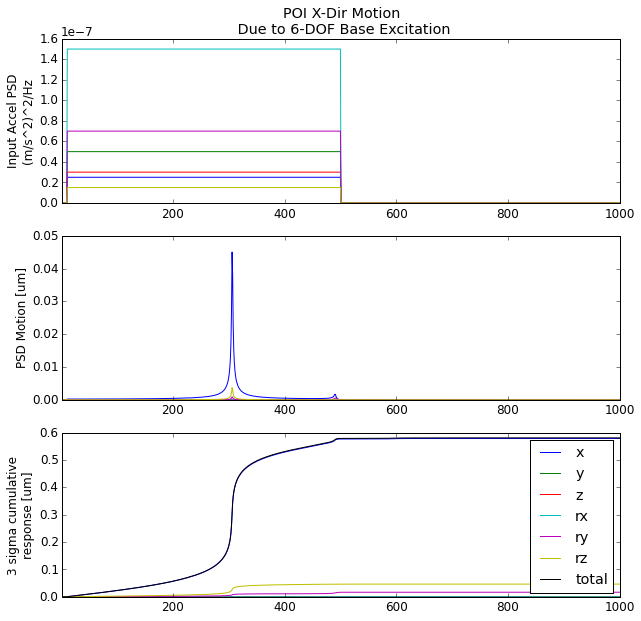
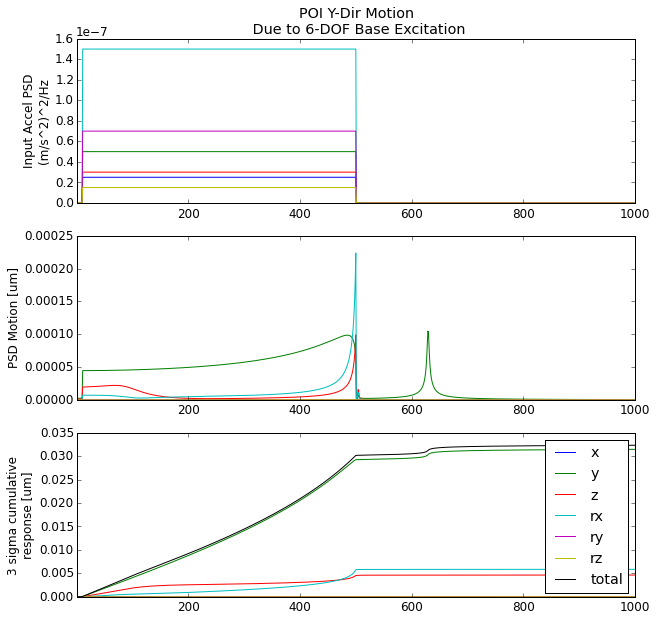
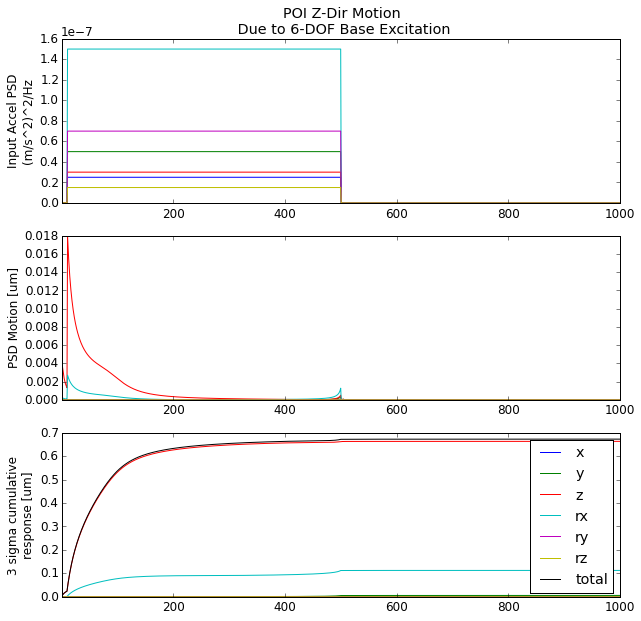
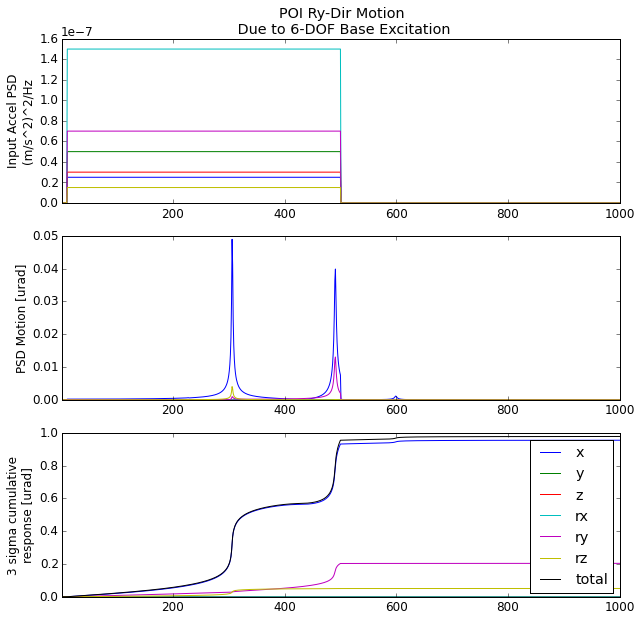
Below are the 6-DOF FRF’s for an input acceleration at the base of the machine and output motion at the poi.
Given the base acceleration levels in the table above, we can estimate the motion of the poi.
For X-dir motion of the POI, we can see that the mode at 302 Hz is the dominant contributor, and we should expect to see about 0.6 μm of motion.
For Y-dir motion of the POI, we can see that most of the motion comes from the y-dir acceleration input across the 0-500Hz frequency range. Note, the mode at 629 Hz is excited but it doesn’t contribute much to the total motion. The “quasi-static” response of the system is the major contributor, if we need to reduce this motion, we should target stiffening the static stiffness in the y-dir. We should expect the POI to move about 0.03 μm due to the base excitation.
For Z-dir motion of the POI we expect to see approximately 0.65 μm motion, and this response is due to the quasi-static stiffness of the system in the z-direction.
For Rx-dir motion of the POI we expect to see about 0.25 μrad tilt and the major contributors are the quasi-static stiffness in the Z and RX direction.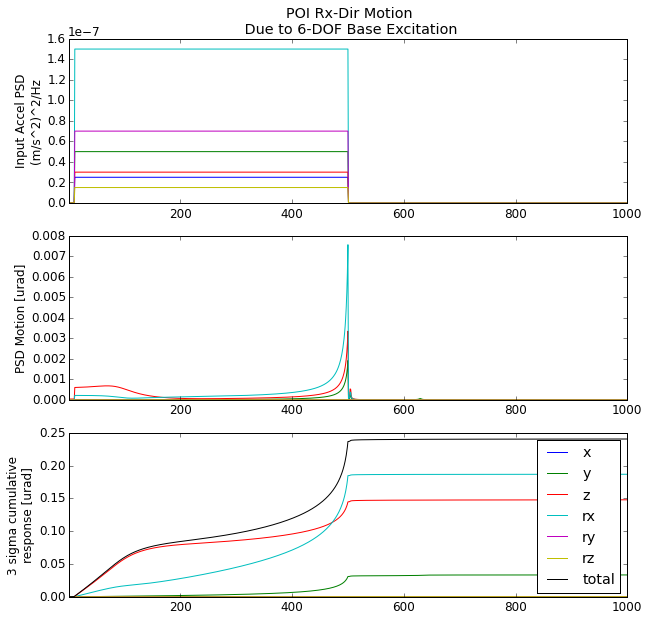
For Ry-dir motion of the POI we expect to see 1 μrad tilt and the major contributors are 306 Hz and 491 Hz modes excited by the X-direction base acceleration.
For Rz-dir motion of the POI we expect to see 2.25 μrad tilt and the major contributor is the 306 Hz mode excited by the X-direction base acceleration.
A summary of the results are in the table below. The system as modeled meets the desired requirements. We would suggest comparing the model to measured date to ensure accuracy. Also we suggest improving the X-dir and Z-dir stability of the system to have a bit more margin on meeting the requirements.
| X-Dir [μm] | Y-Dir [μm] | Z-Dir [μm] | Rx-Dir [μrad] | Ry-Dir [μrad] | Rz-Dir [μrad] | |
|---|---|---|---|---|---|---|
| Stability Reqs. | 1.0 | 1.0 | 1.0 | 5.0 | 5.0 | 50.0 |
| Estimated Stability | 0.60 | 0.03 | 0.65 | 0.25 | 1.0 | 2.25 |